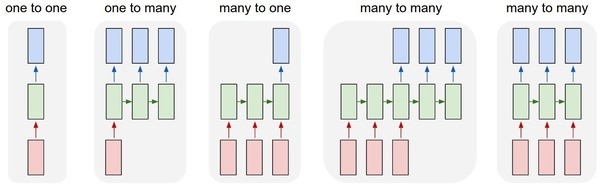
When working with a recurrent neural networks model, we usually use the last unit or some fixed units of recurrent series to predict the label of observations. It was being shown in this picture.

How about choosing some distinct units inside the recurrent (e.g., LSTM, GRU) layer of recurrent neural networks? I have worked on some problem need to do that such as aspect-based sentiment analysis. In this problem, we have to predict the polarity label of some aspect in a sentence or passage. We usually use a tuple (positive, negative or neutral) for the polarity label. E.g:

• single aspect

<text>Love Al Di La</text>
<Opinions>
    <Opinion target="Al Di La" category="RESTAURANT#GENERAL" polarity="positive" from="5" to="13"/>
</Opinions>

• multiple aspects

<text>An awesome organic dog, and a conscious eco friendly establishment.</text>
<Opinions>
    <Opinion target="dog" category="FOOD#QUALITY" polarity="positive" from="19" to="22"/>
    <Opinion target="establishment" category="RESTAURANT#MISCELLANEOUS" polarity="positive" from="53" to="66"/>
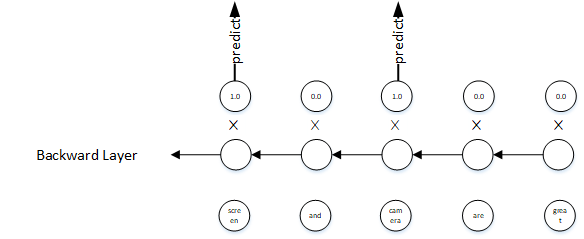
</Opinions>

One of my proposed models is using bidirectional LSTM neural networks. It was being shown in the picture below. In this model, we only predict polarity label for the aspects in the sentence. But we have one problem is the different position of aspects in the different sentence. Uhmm, how will we solve it when we can not use the traditional RNN model?

Here is the solution. We will use an additional masking layer after the LSTM layer. It is a binary vector that ís 1.0 for aspect position, 0.0 for the others. We multiply LSTM layer with masking layer. Then, we compute softmax, cross entropy, and gradient descent as usually.

Here is the Tensorflow code example for this solution:

lstm_fw_cell = tf.nn.rnn_cell.BasicLSTMCell(nb_lstm_inside, forget_bias=1.0)
lstm_bw_cell = tf.nn.rnn_cell.BasicLSTMCell(nb_lstm_inside, forget_bias=1.0)

# pass lstm_fw_cell / lstm_bw_cell directly to tf.nn.bidrectional_rnn
# layers is an int number which is the number of RNNCell we would use
lstm_fw_multicell = tf.nn.rnn_cell.MultiRNNCell([lstm_fw_cell]*layers)
lstm_bw_multicell = tf.nn.rnn_cell.MultiRNNCell([lstm_bw_cell]*layers)

# get lstm cell output
outputs, _, _ = tf.contrib.rnn.static_bidirectional_rnn(lstm_fw_multicell,
                                                        lstm_bw_multicell,
                                                        X_train,
                                                        dtype='float32')

output_fw, output_bw = tf.split(outputs, [nb_lstm_inside, nb_lstm_inside], 2)
sentiment = tf.reshape(tf.add(output_fw, output_bw), [-1, nb_lstm_inside]) 

sentiment = tf.nn.dropout(sentiment, keep_prob)
sentiment = tf.add(tf.matmul(sentiment, sent_w), sent_b)
sentiment = tf.split(axis=0, num_or_size_splits=seq_max_len, value=sentiment)

# change back dimension to [batch_size, n_step, n_input]
sentiment = tf.stack(sentiment)
sentiment = tf.transpose(sentiment, [1, 0, 2])

# tf_X_binary_mask is the masking layer. 
sentiment = tf.multiply(sentiment, tf.expand_dims(tf_X_binary_mask, 2))

cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=sentiment, labels=y_labels))
prediction = tf.argmax(tf.nn.softmax(sentiment), 2)
correct_prediction = tf.reduce_sum(tf.multiply(tf.cast(tf.equal(prediction, tf_y_train), tf.float32), tf_X_binary_mask))

Does masking layer affect the gradient descent when training the model?

Before masking

As far as we know, some of the most important concepts:

• Recurrent Neural Networks

• Cross Entropy Error

\(j\) runs from 1 to 3 because there are three labels (positive, negative and neural) in our example problem.

• Mini-batched SGD

\(B\) is the batch size.

After masking

Consider that \(m\) is the mask vector. Then, we have

If \(m_t = 0\) then \(l_t = 0\). Hence \(\hat{y}_t\) depends on \(W^{(S)}\) only. Moreover, loss function \(J\) depends on \(W^{(S)}\) only too. It does not depend on the none-aspect word \(x_{[t]}\). Finally, the updating process using SGD depends on aspect word mainly because of its impact on softmax layer. So we have solid logic inside the model and it is: “All parameter depends on the aspect mainly, especially for the last softmax layer using \(W^{(S)}\) parameter”.