Spatial Pyramid Pooling (SPP) [1] is an excellent idea that does not need to resize an image before feeding to the neural network. In other words, it uses multi-level pooling to adapts multiple image’s sizes and keep the original features of them. SPP is inspired from:

• Pyramid (image processing)
• Bag-of-words

In this note, I am going to show mathematic inside before porting it into tensorflow version and analyzing upside and downside of it.

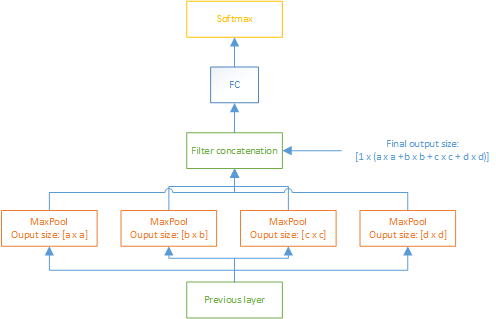
Inside the ideal

Consider that we use n-level pooling (a pyramid) with \(a_1 \times a_1, a_2 \times a_2, ..., a_n \times a_n\) fixed output size correspondingly. Consider that we have an image with size \(h \times w\). After some convolution and pooling layer, we have a matrix features with size \(f_d \times f_h \times f_w\). Then, we apply max pooling multiple times in this matrix features with windows_size \(= \lfloor \frac{f_h}{a_i} \rfloor \times \lfloor \frac{f_w}{a_i} \rfloor\) correspondingly. Easily to see, SPP does not affect to the convolution, fully connected parameters of a neural network model.

We gather all image with the same size to a batch. After that, we train the parameters in each batch, then transfer them to another batch. This is equivalent for the testing scenario.

Tensorflow porting

def spatial_pyramid_pool(previous_conv, num_sample, previous_conv_size, out_pool_size):
    '''
    previous_conv: a tensor vector of previous convolution layer
    num_sample: an int number of image in the batch
    previous_conv_size: an int vector [height, width] of the matrix features size of previous convolution layer
    out_pool_size: a int vector of expected output size of max pooling layer
    
    returns: a tensor vector with shape [1 x n] is the concentration of multi-level pooling
    '''

    for i in range(len(out_pool_size)):
        h_strd = previous_conv_size[0] / out_pool_size[i]
        w_strd = previous_conv_size[1] / out_pool_size[i]
        h_wid = previous_conv_size[0] - h_strd * out_pool_size[i] + 1
        w_wid = previous_conv_size[1] - w_strd * out_pool_size[i] + 1
        max_pool = tf.nn.max_pool(previous_conv,
                                   ksize=[1,h_wid,w_wid, 1],
                                   strides=[1,h_strd, w_strd,1],
                                   padding='VALID')
        if (i == 0):
            spp = tf.reshape(max_pool, [num_sample, -1])
        else:
            spp = tf.concat(axis=1, values=[spp, tf.reshape(max_pool, [num_sample, -1])])
    
    return spp

You can see the full code and an SPP on top of Alexnet example here.

Up-downside

• Creative idea. No need to resize image; also keep original features of an image.
• Take time to gather all image with the same size to a batch.
• Not well working in the high detail requirement identification task. E.g., plant identification, rice identification. Work well on object detection task.
• Sometimes, the loss function can not be converging when using transfer parameters. It may be because of not enough data or the hard level of the problem.

Conclusions

I have just analysis some idea of SPP. SPP is a beautiful idea that combines classic computer visions idea to the modern neural network. Pheww, hope you enjoy it. :D

References

[1] Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition